Sacred Geometry, in my humble opinion, is just awesome. It’s a pretty broad category that contains things like the flower of life and the golden ratio. Today, however, we’re going to focus on the five basic, three-dimensional shapes known as the Platonic Solids. I think this is as good of a place to start as any other.
Fun fact: this was the oldest draft post in my history. I started writing about this topic in May 2023, and have now come back to finish it over a year later.

The Platonic Solids, Wireframe View and Normal View
What are the Platonic Solids? What do they represent? And more importantly… what do we do with them? It’s not just math… there’s magick here! Read on.
The Basic Shapes
In order to qualify as a Platonic Solid, a three-dimensional shape has to meet certain criteria. The technical definition is this: geometric solids whose faces are all identical, regular polygons meeting at the same three-dimensional angles.
Please do not let the technical definition discourage you.
Platonic Solid: Any of five geometric solids whose faces are all identical, regular polygons meeting at the same three-dimensional angles.
For today’s purposes, we’re going to skip all of the math and calculations. The main thing to remember is that we’re talking about a three-dimensional shape that is constructed from two-dimensional shapes. If you do prefer math, however, feel free to jump over to MathWorld’s page where you will find more than you could ever ask for.
There’s obviously lots of ways to connect shapes. The pyramids in Egypt, for example, connect a square base to four triangular sides… but the Egyptian pyramids are not Platonic Solids because they use a combination of two different shapes (a square and triangles).
In order to qualify as a Platonic Solid, all of the faces have to be exactly the same. As a simple example, just picture standard rolling dice like what you would find with a board game or at a casino. Each side of the die is a square and every face is the same.
Are you still with me? Good. Don’t worry, there’s only FIVE shapes that fit this definition. And each one has a correspondence to a particular Element.
Dodecahedron

Element: Spirit
Base Shape: Pentagon (5)
Number of faces: 12
Number of edges: 30
Number of vertices: 20
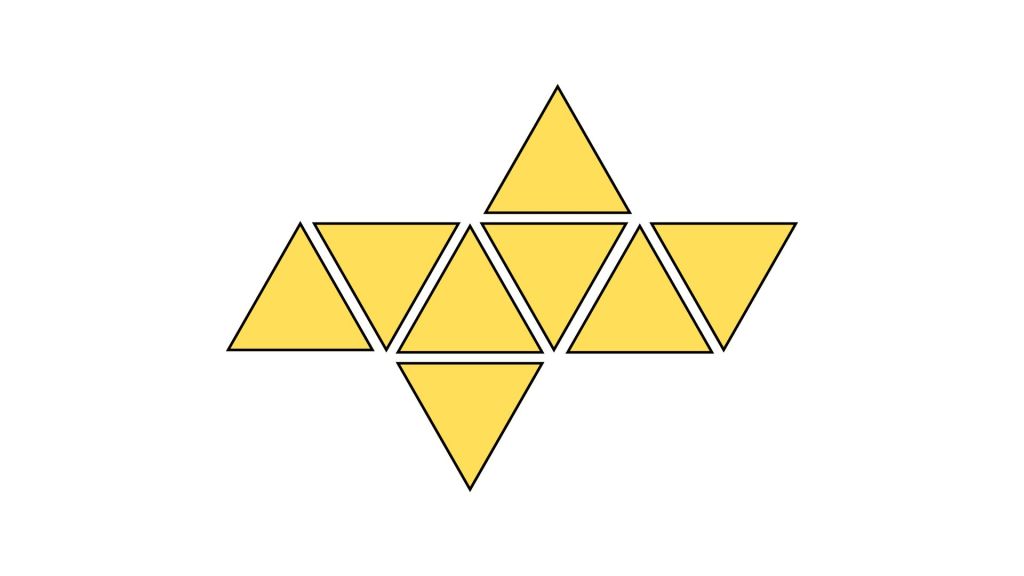
Tetrahedron

Element: Fire
Base Shape: Triangle (3)
Number of faces: 4
Number of vertices: 4
Number of edges: 6
Octahedron
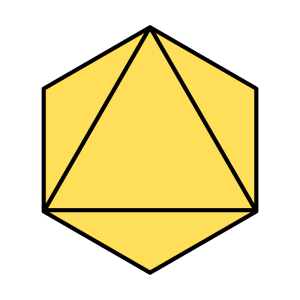
Element: Air
Base Shape: Triangle (3)
Number of faces: 8
Number of vertices: 6
Number of edges: 12
Icosahedron
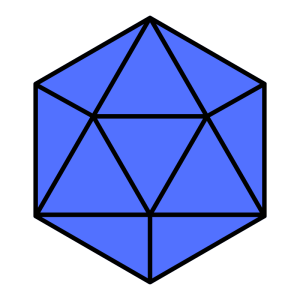
Element: Water
Base Shape: Triangle (3)
Number of faces: 20
Number of vertices: 12
Number of edges: 30
Cube
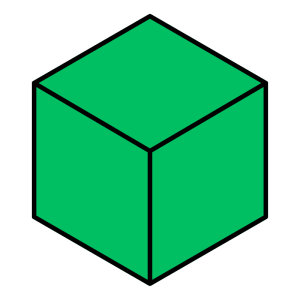
Element: Earth
Base Shape: Square (4)
Number of faces: 6
Number of vertices: 8
Number of edges: 12
Want to hear about future posts? Subscribe to get notifications delivered straight to your inbox.
The cube can also be called a “hexahedron,” by the way, if you want to get all fancy and stuff.
History
Plato is often credited with the Platonic Solids. After all, they’re kind of named after him. But people were probably studying these shapes way before Plato’s time. Carved stone balls dating all the way back to Neolithic times have been found in Scotland, Ireland, and Britain. Some scholars have suggested that this demonstrates ancient people possessed more knowledge of geometry than we might usually give them credit for.

Stone Carvings at Kelvingrove Art Gallery and Museum, picture by Johnbod, CC BY-SA 4.0, courtesy of Wikimedia Commons
But yes, Plato wrote about them in Timaeus in 360 BCE. And he assigned each shape to one of the elements.
The tetrahedron, due to it’s sharp edges and points, was associated with fire. The cube was seen as the most regular and stable, therefore it was associated with earth. The dodecahedron, which has 12 faces, was seen to correspond with the 12 signs of the zodiac, and was associated with the heavens — which we have later taken to mean “spirit.” That just leaves water and air, but the reasoning there gets a little more vague.
Euclid, an ancient greek math guy, pretty much mapped out all of the mathematical properties of the Platonic Solids around 300 BCE, but that didn’t stop people from going even further.
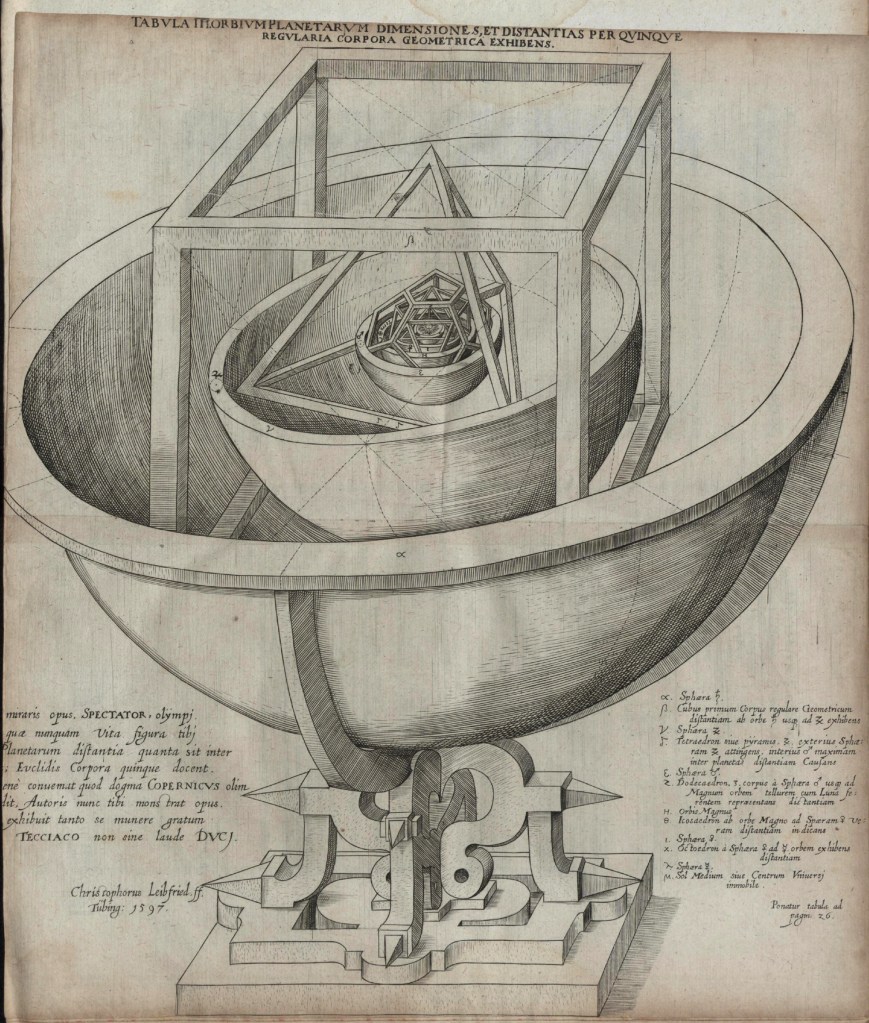
One of Kepler’s Models
Johannes Kepler, a German astronomer, wrote about the Platonic Solids and drew them in Harmonice Mundi in 1619. Kepler’s model of the universe, by the way, was pretty much based on all of the shapes being constructed inside of each other.

Drawings of the Platonic Solids in Harmonice Mundi
Mr. McCall was a pretty big fan of the Platonic Solids as well. You might not know him, but I do. He was my 9th grade Algebra 2/Geometry teacher, so…
Unpacked
Before we go any further, I’d appreciate it if you could take a moment to unpack all of these shapes — that is, visualize them being unfolded into a flat, two-dimensional space.
Don’t worry, I’m actually going to show you pictures as a guide.
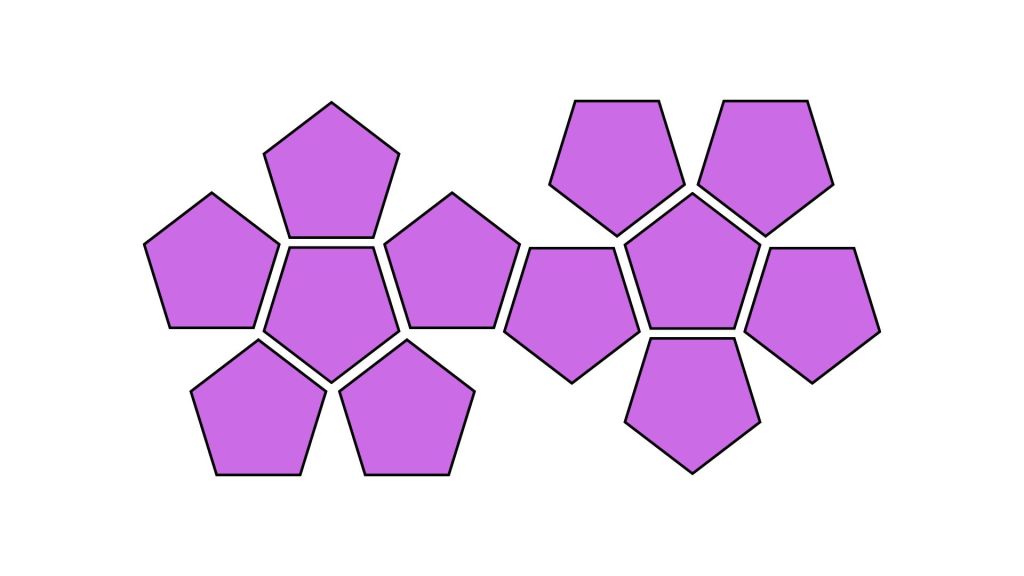
Unfolded Dodecahedron

Unfolded Tetrahedron
Unfolded Octahedron
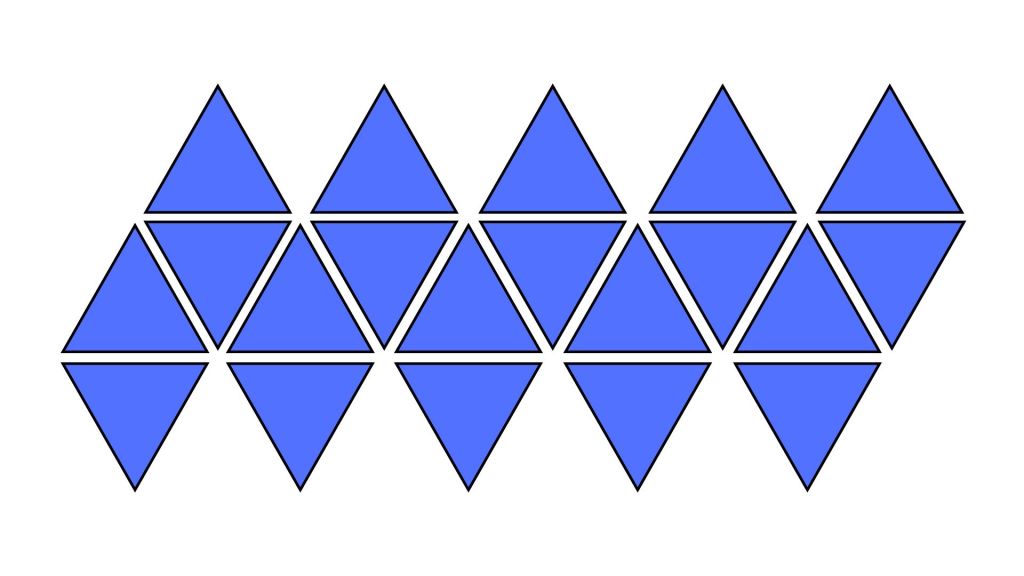
Unfolded Icosahedron
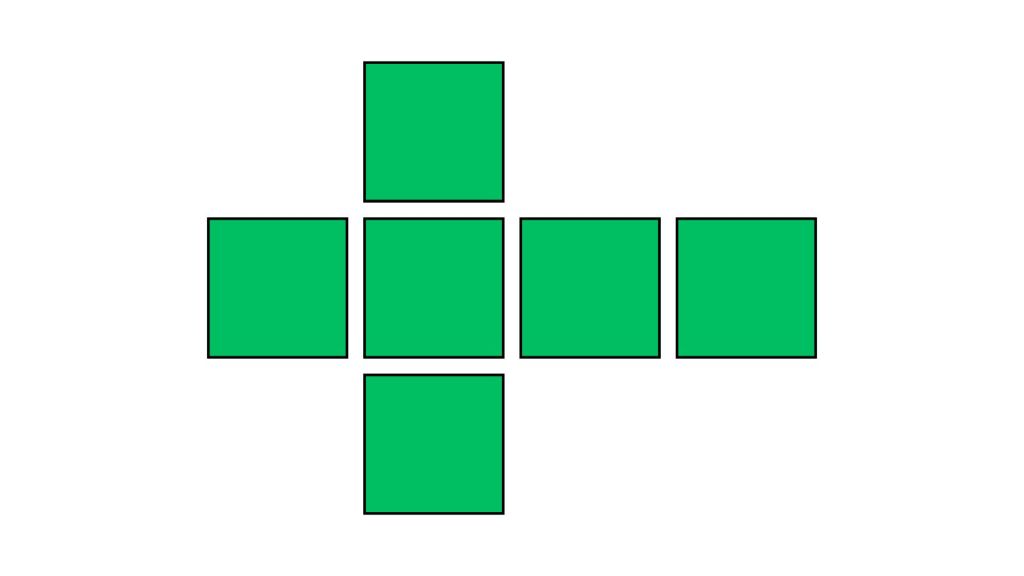
Unfolded Cube
Thank you for taking the time to do that. Seriously. Creating those graphics in Canva took me way longer than it probably should have… and if you hadn’t looked at them just now, then it would have all been for naught.
A Pattern Emerges

You may notice that the dodecahedron for Spirit and the cube for Earth are unlike each other or any of the other shapes. The tetrahedron, octahedron, and icosahedron (fire, air, and water) are all built on triangles.
For the longest time, this progression bothered me. My brain was looking for a logical order — some semblance of a pattern to the numbers that corresponded to the elements they represented. I originally thought that the complexity of the shape (that is, the total number of faces) should directly correspond to its spiritual activity. That would link the tetrahedron (with four faces) to Earth (the least reactive element) and the icosahedron (with twenty faces) to Spirit (the most active of all). That progression doesn’t work… at least not by the classical definitions and associations.
After lots of meditation and thought, I eventually arrived at an explanation. I’ll share it with you, but I should mention that it’s my own journey through the Platonic Solids and it may not match up with other people’s beliefs.
We’re going to take a slightly different approach to the elements today.
Spirit is unique. It is represented as the dodecahedron, whose base shape is a pentagon. The pentagon, with it’s five sides, is unlike any of the other base shapes. This number, five, also aligns with the fifth element, which we might call ether or quintessence, but ultimately the nature of spirit is unknowable.
As the energy of Spirit begins to coalesce, it is refracted and reflected through planes of existence. This changes the base shape. The next three Platonic Solids are built on triangles.
The first emanation is Fire, the most energetic and least dense of any of the four elements. Fire is represented by the tetrahedron, which has the the least number of triangular faces (four) and is the simplest three dimensional solid that can be made.
Fire’s opposite is water. Water is the most crushing and dense of the elements. It is also heavy and complex; therefore it is represented by the icosahedron, which has the most triangular faces (20). The interaction of these two polarities (fire and water) manifests reality, but something must go between them.
Air mitigates the reaction between Fire and Water. As such, it has some properties of each. It is represented by the octahedron with 8 triangular faces (more than Fire, but less than Water) setting it gently between the two extremes.
You can see now that the triangular shape grows in complexity, starting with the Tetrahedron (4) of Fire, moving to the Octahedron (8) of Air, and finally arriving at the Icosahedron (20) of Water. But we don’t end our journey there.
Earth is manifested by the interplay of the other three elements. Just like Spirit, it is distinctly different. And also just like Spirit, the energies are reflected again as they move between planes of existence. This changes the base shape to the final form which has four sides, giving us a cube — the most regular and stable shape.
Maybe that resonates with you. Maybe it doesn’t. But that’s what makes sense to me.
Physical Representations

My crystal set of Platonic Solids
If you’d like to get to know the Platonic Solids better, you have to play with them.
I mean honestly, it doesn’t make a ton of logical sense, but that’s just the way it seems to be. Draw them. Build them. I’ve watched people fold them out of paper or construct wireframe models out of sticks. You need to be able to touch and feel them.
A really simple way to accomplish this is purchase a set of crystals that have been cut to these five shapes. I have one of these sets and it is very helpful. Close your eyes, hold each shape in your hands, feel the edges and points with your fingers.
Seriously. Without having some sort of physical representation of the Platonic Solids, it’s kind of like trying to explain the wetness of water to someone who has never touched water before.
You can find lots of these sets online made out of various materials, even plastic. Do yourself a favor and get one.
Conclusions
We’re just starting our journey. There’s lots more to discuss about the Platonic Solids, like how to meditate with them, construct them in your mind, how each one has a dual, and how they all fit inside of each other.
And on top of that, there’s way more to talk about within the scope of Sacred Geometry.
But that will all have to wait for another day and another post.
In the meantime, let me know what you think. How do you work with the Platonic Solids? How does each one make you feel? Tell me about it in the comments!
It’s that time again. You’ve hit the end of the article. I can already hear you breathing a sigh of sweet relief. Before you finish that exhalation, let me just inform you that there is an Amazon affiliate link somewhere on this page. If you use that link to make a purchase, Amazon will pay me a small commission. That’s just how it works, okay? Okay. Now you can finish your exhalation. Wait, you’re still breathing, right? Hello? Ugh… crap… not again…







Leave a reply to Lara Johnson-Beebe Cancel reply